Plane waves propagate in a homogeneous, non-permeable, but anisotropic dielectric. The dielectric is characterized by a tensor ?_ij, but if coordinate axes are chosen as the principle axes, the components of displacement along these axes are related to the electric-field components by D_i = ?_iE_i(i = 1, 2, 3), where ?_i are the eigenvalues of the matrix ?_ij.

(a) Show that plane waves with frequency a> and wave vector k must satisfy

k ? (k ? ?) + ?₀?²D = 0

(b) Show that for a given wave vector k = kn there are two distinct modes of propagation with different phase velocities v = ?/k that satisfy the Fresnel equation?

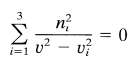
Where v_i = l/??₀?_i is called a principal velocity, and n_i is the component of n along the i-th principal axis.

(c) Show that D_a ? D_b = 0, where D_a, D_b are the displacements associated with the two modes of propagation.

n? =D0=