Question: Project Euler formulas in Terms of Jumps withut Integration; show that for a function whose third derivative is identically zero, where n = 1, 2,

Project Euler formulas in Terms of Jumps withut Integration; show that for a function whose third derivative is identically zero, where n = 1, 2, ??? and we sum over all the jumps js, j's, j''s of f, f', f', respectively, located at xs.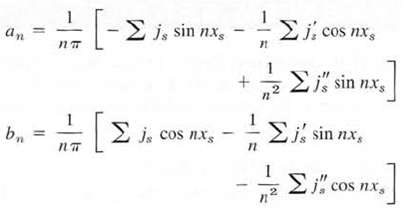 an 11 [- j, sin nxs b, = mm [ j, by

an 11 [- j, sin nxs b, = mm [ j, by cos nxs - + . j. cos nxs ' . ] ;" sin nxs - . j. sin n.., j cos nx. ]

Step by Step Solution

★★★★★

3.37 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

By applying the procedure once more namely to the integral on the right we obtain the jump ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

M-C-D-E (265).docx

120 KBs Word File

Students Have Also Explored These Related Calculus Questions!

Show that for a discrete uniform random variable X, if each of the values in the range of X is multiplied by the constant c, the effect is to multiply the mean of X by c and the variance of X by c2....

Show that for a van der Waals gas, Cp,m Cv,m = R 1/ = 1 (3Vt 1)2/4V3tTt and evaluate the difference for xenon at 25C and 10.0 atm.

Show that for a constant acceleration, 2

8.1. Dulles Electric Company buys 1 million tons of coal annually to burn at its power plant. The company wants to invest in a unit train that will haul coal from the mine to the power house, where...

2.7. Explicit Solutions to Dierential Equations 109 power (kw) 20 15 10 5 0 08:00 10:00 12:00 14:00 16:00 time 18:00 2.7 Explicit Solutions to Dierential Equations In the very rare case in which an...

6.1. Carbondale Company has the following credit policy 2/10, net 30. Carbondale also charges 1% per month interest on all accounts after 30 days. The following table shows the collection schedule of...

re Regular Languages and Finite Automata (a) Let L be the set of all strings over the alphabet {a, b} that end in a and do not contain the substring bb. Describe a deterministic finite automaton...

ANSI-SPARC6 Programming Language Compilation Write notes on each of the following topics: (a) the implementation of labels and jumps in a recursive, block structured programming language [7 marks]...

software projects failed. In the run-up to Y2K, most of the world's large companies claimed that fixing the Millennium Bug was a large project whose success was critical to their survival. One would...

The most critical submission of the theory of computation has been to establish that the halting problem is not decidable. Give a clear statement of this result (you are not asked to prove it). [5...

Landson company is an industrial firm that specialize in producing household cleaning products, steve is the financial manager of the company and one of his strategies to use the extra cash is to...

An experiment was conducted to compare the effects of three toxic chemicals, A, B, and C, on the skin of rats. One-inch squares of skin were treated with the chemicals and then scored from 0 to 10...

Describe some techniques that car salespeople might use in negotiating the price of the car.

Problem 2. Find all the values of the following expressions and determine their principal values. (1) (4- 4V3)4-3 (2) (4i)8i (3) log(e + ei)

a. Three junior portfolio managers Andrew, Betty, and Cornell are arguing on the scenario when they should stop monitoring the portfolio performance. Andrew states that it is when the portfolio is...

Present and future value tables of $1 at 3% are presented below: N FV $1 PV $1 FVA $1 PVA $1 FVAD $1 PVAD $1 1 1.03000 0.97087 1.0000 0.97087 1.0300 1.00000 2 1.06090 0.94260 2.0300 1.91347 2.0909...

In Exercises 1318, calculate the derivative in two ways. First use the Product or Quotient Rule; then rewrite the function algebraically and directly calculate the derivative. (x) = x 3 x 3

Joey realizes that he has charged too much on his credit card and has racked up $4,500 in debt. If he can pay $175 each month and the card charges 15 percent APR (compounded monthly), how long will...

Enter your answer as a decimal number with four digits to the right of the decimal point Listen An experiment is start a new business. A highly informed investment banker thinks the odds are 70-to-10...

We are evaluating a project that costs $986,000, has a life of twelve years, and has no salvage value. Assume that depreciation is straight-line to zero over the life of the project. Sales are...