A real finite-duration sequence whose z-transform has no zeros at conjugate reciprocal pair locations and no zeros on the unit circle is uniquely specified to within a positive scale factor by its Fourier transform phase (Hayes et al., 1980). An example of zeros at conjugate reciprocal pair locations is z = a and (a*) -1. Even though we can generate sequences that do not satisfy the preceding set of conditions, almost any sequence of practical interest satisfies the conditions and therefore is uniquely specified to within a positive scale factor by the phase of its Fourier transform. Consider a sequence x [n] that is real, that is zero outside 0 ? n ? N ? 1, and whose z-transform has no zeros at conjugate reciprocal pair locations and no zeros on the unit circle. We wish to develop an algorithm that reconstructs cx [n] from j?), the Fourier transform phase of x [n], where c is a positive scale factor. ?

(a) Specify a set of (N ? 1) linear equations has a unique solution. Further, show that if we know j?) rather than just tan {j?)}, the sign of the scale factor cal also be determined.

(b) Suppose, using the approach developed in part (a), demonstrate that c_x[n] can be determined from j?), where c is a positive scale factor.

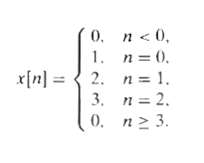
0. 3.