Some consequences of the Maxwell-Boltzmann distribution, in the simplified kinetic theory in S1.4, several statements concerning the equilibrium behavior of a gas were made without proof. In this problem and the next, some of these statements are shown to be exact consequences of the Maxwell-Boltzmann velocity distribution. The Maxwell-Boltzmann distribution of molecular velocities in an ideal gas at rest is f(u_x, u_y, u_z) = n(m/2?kT)^3/2 exp(?mu²/2kT) (1C.1-1) in which u is the molecular velocity, n is the number density, and f(u_x, u_y, u_z)du_x?du_y?du_z is the number of molecules per unit volume that is expected to have velocities between u_x and u_x + du_x, u_y and u_y + du_y, u_z and u_z + du_z. It follows from this equation that the distribution of the molecular speed u is f(u) = 4?nu²(m/2?kT)^3/2 exp(?mu² /2kT)?

(a) Verify Eq. 1.4-1 by obtaining the expression for the mean speed u from

(b) Obtain the mean values of the velocity components u_x, u_y, and u_z. The first of these is obtained from what can one conclude from the results?

(c) Obtain the mean kinetic energy per molecule by the correct result is ? mu² = 3/2kT.

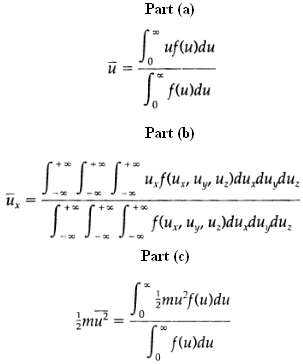
Ux Part (a) Suf(u)du 0 fflurdu Part (b) u.f(u, u, u.)du du du. ** ** ** f(u, u, udududu. Part (c) mu S* \muf(u)du S flurdu