A permutation matrix is one that can be obtained from an identity matrix by reordering its rows. If P is an n x n permutation matrix and A is any n x n matrix and C = PA, then C can be obtained from A by making precisely the same reordering of the rows of A as the reordering of the rows which produced P from I_n. 

a. Show that every finite group of order n is isomorphic to a group consisting of n x n permutation matrices under matrix multiplication. 

b. For each of the four elements e, a, b, and c in the Table 5.11 for the group V, give a specific 4 x 4 matrix that corresponds to it under such an isomorphism.

Table 5.11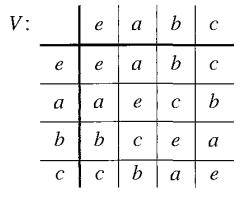

V: e a b e a a e b e ab C bc C b C b C e a b a e