Consider K = Q(√2, √3). Referring to Exercise 17, compute each of the following (see Example 53.3).

a. N_k/Q(√2)

b. N_K/Q(√2 +√3)  

c. N_K/Q(√6)

d. N_K/Q(2)

e. Tr_k/Q(√2)

f. Tr_k/Q(√2 + √3)

g. Tr_K/Q(√6)  

h. Tr_k/Q(2)

Data from Exercise 17

Let K be a finite normal extension of a field F. Prove that for every α ∈ K, the norm of α over F, given by

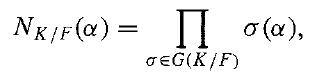
and the trace of α over F, given by

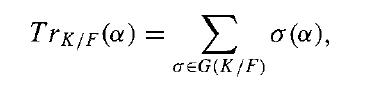
are elements of F.

Data from 53.3 Example

Let K = Q(√2, √3). Now K is a normal extension of Q, and Example 48.17 showed that there are four automorphisms of K leaving Q fixed. We recall them by giving their values on the basis {1, √2, √3, √6} for K over Q.

ι : The identity map

σ₁: Maps √2 onto -√2, √6 onto -√6, and leaves the others fixed

σ₂ : Maps √3 onto -√3, √6 onto -√6, and leaves the others fixed

σ₃ : Maps √2 onto -√2, √3 onto -√3, and leaves the others fixed

We saw that {i, σ₁, σ₂, σ₃} is isomorphic to the Klein 4-group. The complete list of subgroups, with each subgroup paired off with the corresponding intermediate field that it leaves fixed, is as follows:

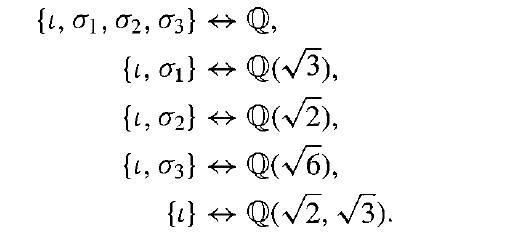
Nx/F(a) = (), G(K/F)