Question: Let R = {a + b2 | a, b Z} and let R' consist of all 2 x 2 matrices of the form Show

Let R = {a + b√2 | a, b ∈ Z} and let R' consist of all 2 x 2 matrices of the form[a b] for a, b Z.

Show that R is a subring of !R. and that R' is a subring of M2(Z). Then show that ∅ : R → R', where ∅(a + b√2) =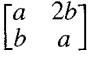

ls an isomorphism.

[a b] for a, b Z.

Step by Step Solution

★★★★★

3.30 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Because a b2c d2 a cb d 2 and 0 0 02 and a b2 ab2 we see tha... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related A First Course In Abstract Algebra Questions!

Q:

Let z = ((x, y), where x = r cos ( and y = r sin (. Show that dr

Q:

Let A and B be 2 Ã 2 matrices and let (a) Show that det(A + B) = det(A) + det(B) + det(C) + det(D). (b) Show that if B = EA then det(A + B) = det(A) + det(B). D-I 12 a21 a22

Q:

Let A and B be n x n matrices and let x be a vector in Rn. How many scalar additions and multiplications are required to compute (AB)x and how many are necessary to compute A(Bx)? Which computation...

Q:

a 3b 9. Let R = {a + bv3 a, b E Z} and R' the 2 x 2 matrices b a where a, b E Z. a. Show that R is a subring of R. b. Show that R' is a subring of M2 (Z). c. Show that p: R - R' by p(a + bv3 = is a...

Q:

Homework 4 Starting Mutation A set of tests will be supplied to you, but you should still make tests to ensure that your functions are performing the operations you anticipate. For a full grade, you...

Q:

HELP WITH CODING IN PLAIT LANGUAGE USING DrRacket: Homework 4 Starting Mutation A set of tests will be supplied to you, but you should still make tests to ensure that your functions are performing...

Q:

11. Let A={1,2,3} and B={1,2,3,4}. Let R and S be the relations from A to B whose matrices are given. ComputeR( )S 0 MR = 10 0 0 0 0 0 0 C A. {(1,1), (2,4), (3,2)} B. {(1,1), (1,3), (2,4), (3,2)} C...

Q:

An axis aligned rectangle classifier in the plane is a classifier that assigns the value 1 to a point if and only if it is inside a certain rectangle. Formally, given real numbers a

Q:

logic and discrete structures sample answer for this sort of questions: (3) Determine the truth-values of the following. Give reasons. (a) Vry : x + y = 1 for x,y E Z (b) Vx,y e R+ : V= y (c) 3x Z,...

Q:

Help me pls 30. 31. 32. 33. 34. 35. 36. 3'7. 38. 39. 40. 41. 42. 43. Suppose that there is an integer n > 1 such thatx\" = x for all elements x of some ring. If m is a positive integer and am = 0 for...

Q:

Suppose that Y1, Y2, . . ., Yn is a random sample of size n drawn from a continuous pdf, fY(y), whose median is m. Is P(Y1 > m) less than, equal to, or greater than P(Yn > m)?

Q:

1:B2B company for renting modern office space for small businesses is trying to decide which segment of customers it should enter. The options for it are divided into three segments: (a)...

Q:

Swifty Mining Corp. has the following account balances related to its mining operations: \ table [ [ Accumulated depreciation - mineral property,$ 3 , 6 3 4 , 0 0 0

Q:

4. What are the contributions of the right hemisphere to emotional behaviors and interpreting other peoples emotions?

Q:

According to the Bureau of the Census, 19.0% of the U.S. population lives in the Northeast, 22.9% in the Midwest, 35.6% in the South, and 22.5% in the West. In a random sample of 200 recent calls to...

Q:

It has been reported that 10.3% of U.S. households do not own a vehicle, with 34.2% owning 1 vehicle, 38.4% owning 2 vehicles, and 17.1% owning 3 or more vehicles. The data for a random sample of 100...

Q:

Approximately 13.3% of U.S. drivers are younger than age 25, with 39.2% in the 2544 age group, and 47.5% in the 45-and-over category. For a random sample of 200 fatal accidents in her state, a safety...

Q:

3710 (1.) Consider the following information: Portfolio Risk-free Market Expected Standard Return Deviation 10% 18 24 20 22 a. Calculate the Sharpe ratios for the market portfolio and portfolio A....

Q:

Caps Ltd sells hats and other head-wear in malls and makes a variety of custom products for clients. The company recently decided to focus more on manufacturing custom products in small to medium...

Q:

8. (Ex-ante and ex-post risk and return) During a finance lecture, Professor Johnson explained to his students the relation between higher risk and higher expected returns. At the end of the lecture,...