Show by a construction analogous to that given in the proof of Theorem 47.4 that the division algorithm holds in the integral domain Z[√-2] for v(α) = N(α) for nonzero α in this domain (see Exercise 16). (Thus this domain is Euclidean. See Hardy and Wright [29] for a discussion of which domains Z[√n] and Z[√-n] are Euclidean.)

Data from Theorem 47.4

The function v given by v(α) = N(α) for nonzero α ∈ Z[i] is a Euclidean norm on Z[i]. Thus Z[i] is a Euclidean domain.

Proof: Note that for B = b₁ + b₂i ≠ 0, N(b₁ + b₂i) = b₁² + b₂², so N(B) ≥ 1. Then for all α, β ≠ 0 in Z[i], N(α) ≤ N(α)N(β) = N(αβ). This proves Condition 2 for a Euclidean norm in Definition 46.1. It remains to prove the division algorithm, Condition 1, for N. Let α, β ∈ Z[i], with
a = a₁ + a₂i and β = b₁ + b₂i, where β ≠ 0. We must find σ and ρ in Z[i] such that α= βσ + ρ, where either ρ = 0 or N(ρ) < N(β) = b₁² + b₂². Let α/β = r + si for r, s ∈ Q. Let q₁ and q₂ be integers in Z as close as possible to the rational numbers r and s, respectively. Let σ = q₁ + q₂i and ρ = α - βσ. If p = 0, we are done. Otherwise, by construction of σ, we see that |r - q₁|≤ ½ and |s - q₂| ≤ 1/2. Therefore 

Thus we obtain

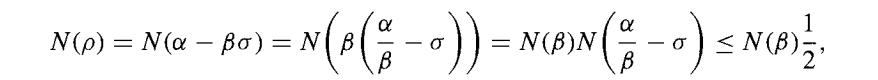
so we do indeed have N(ρ) < N (β) as desired.

Transcribed Image Text:

N ( 2 1 - 0) В = = N((r+si) (91 +92i)) - 2 2 1 = = N((r — q₁) + (s— q2)i) ≤ € (1) ² + ( 1 ) ² = ²/ 2 2