Show that x⁴ + 1 is irreducible in Q[x], as we asserted in Example 54.7.

Data from in 54.7 Example 

Consider the splitting field of x⁴ + 1 over Q. By Theorem 23.11, we can show that x⁴ + 1 is irreducible over Q, by arguing that it does not factor in Z[x]. (See Exercise 1.) The work on complex number in Section 1 shows that the zeros of x⁴ +1 are (1 ± i)/√2 and (-1 + i)/√2. A computation shows that if

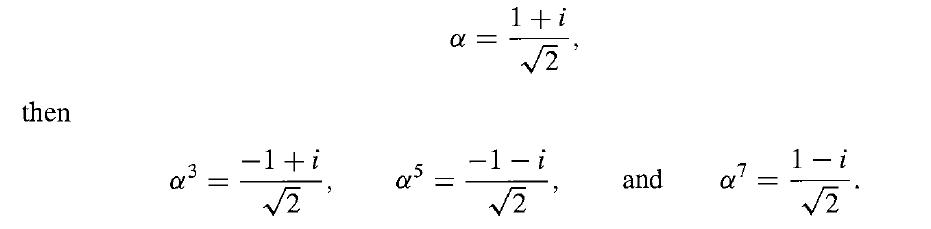
Thus the splitting field K of x⁴ + 1 over Q is Q(α), and [K : Q] = 4. Let us compute G(K/Q) and give the group and field diagrams. Since there exist automorphisms of K mapping α onto each conjugate of α, and since an automorphism σ of Q(α) is completely determined by σ(α), we see that the four elements of G(K/Q) are defined by Table 54.8. Since (σ_jσ_k)(α) = σ_j(α^k) = (α^j)^k = a^jk and α⁸ = 1, we see that G(K/Q) is isomorphic to the group {1, 3, 5, 7} under multiplication modulo 8. This is the group G₈ of Theorem. 20.6. Since σ²_j = σ₁, the identity, for all j, G(K/Q) must be isomorphic to the Klein 4-group. The diagrams are given in Fig. 54.9.

Transcribed Image Text:

then Q³ −1+i √2 a5 α || - 1 + i √2 1- i √2 > and a² = 1- i √2