Question: (a) Give a proof of Weierstrass M-test. (b) Derive Theorem 4 from Theorem 3. (c) Prove that uniform convergence of a series in a region
(a) Give a proof of Weierstrass M-test.
(b) Derive Theorem 4 from Theorem 3.
(c) Prove that uniform convergence of a series in a region G implies uniform convergence in any portion of G. Is the converse true?
(d) Find the precise region of convergence of the series in Example 2 with x replaced by a complex variable z.
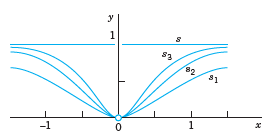
(e) Show that x2 Σˆžm=1 (1 + x2)-m = 1 if x ‰ 0 and 0 if x = 0. Verify by computation that the partial sums s1, s2, s3 look as shown in Fig. 369
82 81 -1
Step by Step Solution
3.47 Rating (163 Votes )
There are 3 Steps involved in it
a Convergence follows from the comparison test Sec 151 Let R n z and R n be the remain... View full answer

Get step-by-step solutions from verified subject matter experts


