(a) Show that u_n= rⁿcos nθ, u_n= rⁿsin nθ, n = 0, 1,· · ·, are solutions of Laplace€™s equation ˆ‡²u = 0 with ˆ‡²u given by (5). (What would u_nbe in Cartesian coordinates? Experiment with small n.)

(b) Solve the Dirichlet problem using (20) if R = 1 and the boundary values are u(θ) = -100 volts if -π < θ < 0, u(θ) = 100 volts if 0 < θ < π. (Sketch this disk, indicate the boundary values.)

(c) Show that the solution of the Neumann problem ˆ‡²u = 0 if r < R, u_N(R, θ) = f (θ) (where u_N = ˆ‚u/ˆ‚N is the directional derivative in the direction of the outer normal) is

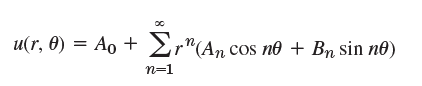
with arbitrary A₀ and

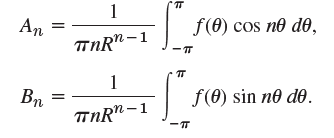
(d) Solve ˆ‡²u = 0 in the annulus 1 < r < 2 if u_r (1, θ) = sin θ, u_r (2, θ) = 0.

u(r, 0) = Ao + Er"(An cos no + Bn sin n) n=1 An f (0) cos n d, -1 nR- Bn nR*-1 f (0) sin n d. -