(a) Solve the initial value problem y" + y = cos ?t, ?² ? 1, y(0) = 0, y' (0) = 0. Show that the solution can be written

(b) Experiment with the solution by changing ? to see the change of the curves from those for small ? (>0) to beats, to resonance, and to large values of ? (see Fig. 60).

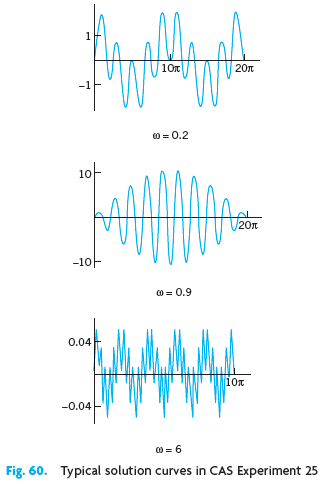
y (t) 2 1-w sin [(1 + w)t] sin (1-w)t]. 10/ -10- 0.04 -0.04 AM V0A 10t O=0,2 CO= 0.9 20t Hote 20T 10x 00=6 Fig. 60. Typical solution curves in CAS Experiment 25