(a) Write a program for Gauss–Seidel iteration.

(b) Apply the program A(t)x = b, to starting from [0    0    0]^T, where

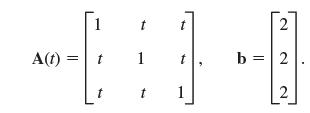
For t = 0.2, 0.5, 0.8, 0.9 determine the number of steps to obtain the exact solution to 6S and the corresponding spectral radius of C. Graph the number of steps and the spectral radius as functions of t and comment.

(c) Show that by adding and subtracting x^(m) on the right, formula (6) can be written

Anticipation of further corrections motivates the introduction of an over relaxation factor ω > 1 to get the SOR formula for Gauss–Seidel

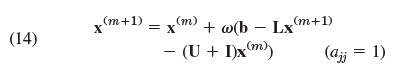
intended to give more rapid convergence. A recommended value is ω = 2/(1 + √1 - ρ) where ρ is the spectral radius of C in (7). Apply SOR to the matrix in (b) for t = 0.5 and 0.8 and notice the improvement of convergence. (Spectacular gains are made with larger systems.)