Find the linear fractional transformation z g(Z) that maps Z 1 onto z 1 with Z i 2 being mapped onto z 0 Show that Z 1 0 6 0 8i is mapped onto z 1 and Z 2 0 6 0 8i onto z 1, so that the equipotential lines of Example 2 look in Z 1 as shown in Fig 407

Question: Find the linear fractional transformation z = g(Z) that maps |Z| 1 onto |z| 1 with Z = i/2 being mapped onto z

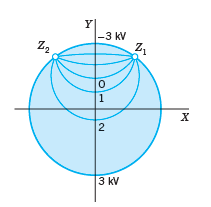
Find the linear fractional transformation z = g(Z) that maps |Z| ≤ 1 onto |z| ≤ 1 with Z = i/2 being mapped onto z = 0. Show that Z₁ = 0.6 + 0.8i is mapped onto z = -1 and Z₂ = -0.6 + 0.8i onto z = 1, so that the equipotential lines of Example 2 look in |Z| ≤ 1 as shown in Fig. 407.

$Find the linear fractional transformation z = g(Z) that maps |Z| ≤$

Step by Step Solution

★★★★★

3.41 Rating (167 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Solution The linear fractional transformation i2 maps Z 1 onto z 1 z i2 is mapped onto z 0 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Advanced Engineering Mathematics Questions!

The neural structure of the sea slug Aplysia has been widely studied (first by Nobel Laureate Eric Kandel) because it has only about 20,000 neurons, most of them large and easily manipulated....

Find complex numbers t = z1 + z2 and s = z1 - z2, both in polar form, for each of the following pairs: (a) z2 2 + j3, z2 1 j3, (b) z1 3, z2 - - j3, (c) z1 0- 330, z2 3 -30, (d) z1 3 30, z2 3...

Show that in Example 2 the y-axis is mapped onto the unit circle in the w-plane.

Show that if Re z1 > 0 and Re z2 > 0, then Log(z1z2) = Log z1 + Log z2.

25. Letz=m+iy andw=u+iv. (1) Find the linear fractional transformation to = f (2) that maps the points 1, 2', 1 to the points z', 0, 2', respectively. (ii) What is the image under f of the unit...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Review Problems 3 Four FIR Filter Types Four types of FIR linear phase digital filters have coefficients h(n) for 0 n M. They are defined as follows: Type I: h(n) = h(M-n) and M even. Type II: h(n) =...

Ryan Ren Assignment Homework 2 due 09/14/2017 at 02:15pm PDT 1. (1 pt) Compute the following product. \u0014 \u0015\u0014 \u0015 \u0014 5 0 4 7 4 = 0 7 1 7 7 Math4A-02-M17-Wen \u0015 Answer(s)...

Pavolia Inc. is a restaurant that specializes in turkey burgers. The company is 100% owned by the owner-manager, Anna. In addition to the restaurant, the company also owns a small rental property...

Develop an equation for the System Stiffness Matrix [K] while designing the steel structure.

xYou are short a European Call option on Tesla with a strike of $ 2 7 5 . Option premium was $ 2 5 . The option can not be sold on secondary markets and thus must either be exercised on expiry or...

15. Refer to the advice on page 140, and revise the following sentences to eliminate the dangling modifiers. a. By following these instructions, your computer should provide good service for many...

The number of police calls a small police department received each month is shown in the frequency distribution. Class limits Frequency 39.942.8 2 42.945.8 2 45.948.8 5 48.951.8 5 51.954.8 12...

The frequency distribution shows the number of days it took to fix each of 80 computers printers. Class limits Frequency 13 7 46 9 79 32 1012 20 1315 12 80 a. Construct a percentile graph. b. Find...

The data show the number of named storms for the years 18511860 and 1941 and 1950. Construct a boxplot for each data set and compare the distributions. 18511860 19411950 6 5 8 5 5 6 4 6 10 10 11 11 6...

A bond currently sells for $925, has 7 years left to maturity and pays a 9% annual coupon What is the YTM? Select one: O A. 11.25% OB. 9% O C. 10.57% OD 8.48% Coupon interest rates determine? Select...

You observe the following yield curve for Treasury securities: Assume that the pure expectations hypothesis holds. What does the market expect will be the yield on 3-year securities, 2 year from...

Which of the following journal entries is correct for Smith Company when Smith issues 10, 300 shares of $10 par value common stock and pays $20, 300 cash in exchange for a building? The market price...