This method uses the trapezoidal rule and gains precision step wise by halving h and adding an error estimate. Do this for the integral of f(x) = e^-xfrom x = 0 to x = 2 with TOL = 10^-3, as follows.

Apply the trapezoidal rule (2) with h = 2 (hence n = 1) to get an approximation J₁₁. Halve h and use (2) to get J₂₁ and an error estimate

If |ϵ₂₁| ‰¤ TOL, stop. The result is J₂₂ = J₂₁ + ϵ_21.

Show that ϵ₂₁ = 0.066596, hence |ϵ₂₁| > TOL and go on. Use (2) with h/4 to get J₃₁ and add to it the error estimate ϵ₃₁ = 1/3(J₃₁ - J₂₁) to get the better J₃₂ = J₃₁ + ϵ₃₁. Calculate

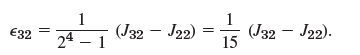
If |ϵ₃₂| ‰¤ TOL, stop. The result is J₃₃ = J₃₂ + ϵ₃₂. (Why does 2⁴ = 16 come in?) Show that we obtain ϵ₃₂ = 0.000266, so that we can stop. Arrange J- and ϵ-values in a kind of €œdifference table.€

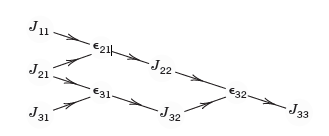
If |ϵ₃₂| were greater than TOL, you would have to go on and calculate in the next step J₄₁ from (2) with then h = 1/4; then

where 63 = 2⁶ - 1. (How does this come in?)

Apply the Romberg method to the integral of f(x) = 1/4Ï€x⁴cos 1/4Ï€x from x = 0 to 2 with TOL = 10^-4.

(J21 J11). 22 1 21 32 24 (J32 J22) 15 (J32 - J22).