Given the function \(f(x)=\frac{1}{a} e^{-|x| / a}= \begin{cases}\frac{1}{a} e^{-x / a} & \text { for } x>0, \\ \frac{1}{a} e^{x / a} & \text { for } x
(a) Show that the Fourier transform of this function \(f(x)\) is \(F(w)=\) \(\sqrt{\frac{2}{\pi}}\left[\frac{1}{1+(w a)^{2}}ight]\).
(b) Recover \(f(x)\) by evaluating the inverse Fourier transform \(\mathscr{F}^{-1}\{F(w)\}\) for the function \(F(w)\) given in part (a) based on a contour integration method (see also Chapter 10). Hint: Consider the contour integral
\[
\frac{1}{\pi a^{2}} \oint_{C} \frac{e^{i z x}}{\left(z+\frac{i}{a}ight)\left(z-\frac{i}{a}ight)} d z
\]
where the contours \(C_{1}\) and \(C_{2}\) are given in Fig. 3.13(a) and Fig. 3.13(b) for \(x>0\) and \(x

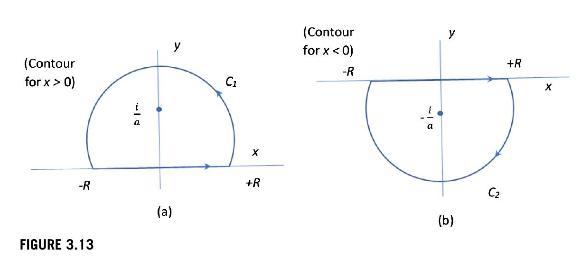
Contours for the integral (a) for the case that \(x>0\) and (b) for the case that \(x

(Contour for x > 0) -R FIGURE 3.13 (a) K C X +R (Contour for x < 0) y (b) C +R X