Let D be a unique factorization domain with a finite number of units and quotient field F. If ∫ ϵ D[x] has degree n and c_o,c₁, ... , c_n are n + 1 distinct elements of D, then ∫ is completely determined by ∫(c₀),∫(c_i), ... , ∫(c_n) according to Exercise 11. Here is Kronecker's Method for finding all the irreducible factors of Jin D[x].

(a) It suffices to find only those factors g of degree at most n/2.

(b) If g is a factor of ∫, then g(c) is a factor of ∫(c) for all c ϵ D.

(c) Let m be the largest integer ≤ n/2 and choose distinct elements c_o,c1, .. . , C_m ϵ D. Choose d_o,d₁, ... , d_m ϵ D such that d_i is a factor of ∫(c_i) in D for all i. Use Exercise 12 to construct a polynomial g ϵ F[x] such that g(c_i) = d_i for all i; it is unique by Exercise 11.

(d) Check to see if the polynomial g of part (c) is a factor of ∫ in F[x]. If not, make a new choice of d_o, ... , d_m and repeat part (c). (Since D is a unique factorization domain with only finitely many units there are only a finite number of possible choices for d_o, ... , d_m.) If g is a factor of ∫, say ∫ = gh, then repeat the entire process on g and h.

(e) After a finite number of steps, all the (irreducible) factors of ∫ in F[x] will have been found. If g ϵ F[x] is such a factor (of positive degree) then choose r ϵ D such that rg ϵ D[x] (for example, let r be the product of the denominators of the coefficients of g). Then r^-1(rg) and hence rg is a factor of ∫. Then rg = C(rg)g₁ with g₁ ϵ D[x] primitive and irreducible in F[x]. By Lemma 6.13, g₁ is an irreducible factor of ∫ in D[x]. Proceed in this manner to obtain all the non constant irreducible factors of ∫; the constants are then easily found. 

Data from Exercise 11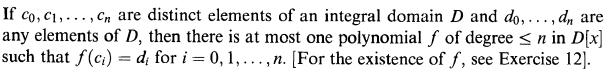

Data from Exercise 12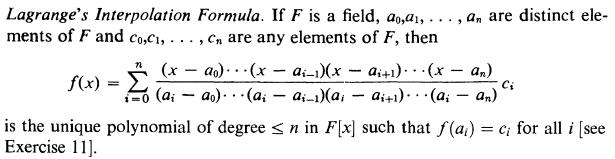

Data from Lemma 6.13

Let D be a unique factorization domain with quotient field F and fa  primitive polynomial of positive degree in D[x]. Then f is irreducible in D[x] if and only  if f is irreducible in F[x].