A needle of length 1 unit is dropped on a floor that is ruled with parallel lines, 1 unit apart. [See Fig. 3.] Let P be the lowest point of the needle, y the distance of P from the ruled line above it, and θ the angle the needle makes with a line parallel to the ruled lines. Show that the needle touches a ruled line if, and only if, y ≤ sin θ. Conclude that the probability of the needle touching a ruled line is the probability found in Exercise 15.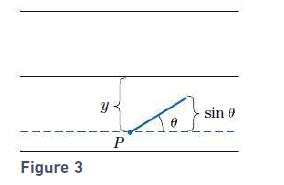

Exercise 15.

A point is selected at random from the rectangle of Fig. 2; call its coordinates (θ, y). Find the probability that y ≤ sin θ.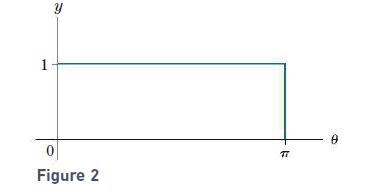

Figure 3 y P - sin 9 0