Question: Let be a convergent series with sum S, and let c be a constant. Then, is a convergent series whose sum is c S.

Let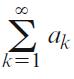k=1

be a convergent series with sum S, and let c be a constant. Then,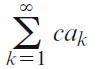

is a convergent series whose sum is c · S. Make a geometric picture to illustrate why this is true when c = 2 and the terms ak are all positive.

k=1

Step by Step Solution

★★★★★

3.36 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

When the height of each rectangle is do... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Applied Calculus Questions!

Q:

The following property is true for any two series (with possibly some negative terms): Let be convergent series whose sums are S and T, respectively. Then, is a convergent series whose sum is S + T....

Q:

KYC's stock price can go up by 15 percent every year, or down by 10 percent. Both outcomes are equally likely. The risk free rate is 5 percent, and the current stock price of KYC is 100. (a) Price a...

Q:

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

Q:

8.1. Dulles Electric Company buys 1 million tons of coal annually to burn at its power plant. The company wants to invest in a unit train that will haul coal from the mine to the power house, where...

Q:

6.1. Carbondale Company has the following credit policy 2/10, net 30. Carbondale also charges 1% per month interest on all accounts after 30 days. The following table shows the collection schedule of...

Q:

1.) Determine whe her the series is convergent or divergent. 00 511 W 4 71 n' :1 ) 911 W 7 71:1 The series ? v Justication: (If more than one test is appropriate, pick the first applicable test in...

Q:

Sy 0.4 0 (16 Vid Slo 2 Los VA X Wa Wa Wa Wa O Ma | Sec TO Ho Ho & Cal 2% Lat Ly De Lat Co TO M Hi E pe + C webassign.net/web/Student/Assignment-Responses/last?dep=30037151 Determine whether the...

Q:

Section 10.5 Reading Assignment: Absolute Convergence; The Ratio and Root Tests Answer Only Exercise 1, 2, and 3 by using a screenshot provided Calculus Pearson textbook. Make sure you read these...

Q:

9New Tab X 12.3 Hmwk-G X VA 12.3 Hmwk-G X (13) gartic ph X G octane apex c X G Google Docs: X E Google Docs X _ Homework#1 X + X...

Q:

5. [10.08 Points] DETAILS SCALCET9 11.2.012. 0/100 Submissions Used MY NOTES ASK YOUR TEACHER Find at least ten partial sums of the series. (Round your answers to ve decimal places.) y y 01.0 - CD...

Q:

Upon activation by a receptor, a G protein exchanges bound GDP for GTP, rather than phosphorylating GDP that is already bound. Similarly, the subunit-GTP complex has a slow GTPase activity that...

Q:

Suppose that the statement ((PAQ) V R) = (R v S) is false. Find the truth values of P, Q, R, and S. (This can be done without making a big truth table if you don't want to, just explain your...

Q:

What is your area of expertise?

Q:

46. Suppose you have a 100GB database housed on a disk array that supports a transfer rate of 60MBps and a tape drive that supports 200GB cartridges with a transfer rate of 80MBps. How long will it...

Q:

For the random variables X and Y in Exercise 2.31 on page 72, determine the correlation coefficient between X and Y. Exercise 2.31 From a sack of fruit containing 3 oranges, 2 apples, and 3 bananas,...

Q:

Random variables X and Y follow a joint distribution Determine the correlation coefficient between X and Y. S2, 0

Q:

Repeat Exercise 2.83 on page 88 by applying Theorem 2.5 and Corollary 2.6. Exercise 2.83 The length of time, in minutes, for an airplane to obtain clearance for takeoff at a certain airport is a...

Q:

RadCo is considering two projects. The first, project A , has $ 4 0 0 , 0 0 0 income after the first year which increases by 8 % each year for a total of 5 years. Project B has $ 4 5 0 , 0 0 0 income...

Q:

You have been hired by an inventor of a new power cell for cars, trucks, and boats, who has some inquiries from prospective investors who would like to know more about the invention before they put...

Q:

What, if anything, should you do to correct the following sentence? He has the ability to affect the outcome, but he's not likely to take that chance. A. Nothing. The sentence is correct as it stands...