Question: Let p(t) = 0.0375t 2 + 0.225t be the density function for the shelf life of a brand of banana, with t in weeks and

Let p(t) = −0.0375t² + 0.225t be the density function for the shelf life of a brand of banana, with t in weeks and 0 ≤ t ≤ 4. See Figure 7.19.

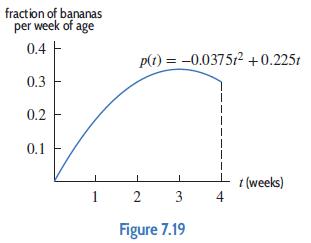
$fraction of bananas per week of age 0.4 0.3 0.2 0.1 1$

(a) Sketch the cumulative distribution function for the shelf life of bananas.
(b) Use the cumulative distribution function to estimate the probability that a banana lasts between 1 and 2 weeks. Check with Problem 16(a).

fraction of bananas per week of age 0.4 0.3 0.2 0.1 1 p(t) = -0.03751 +0.225t 2 3 Figure 7.19 4 t (weeks)

Step by Step Solution

★★★★★

3.46 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The cumulative distribution Pt is the function whos... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Applied Calculus Questions!

Let p(t) = 0.0375t 2 + 0.225t be the density function for the shelf life of a brand of banana, with t in weeks and 0 t 4. See Figure 7.19. Find the probability that a banana will last (a) Between 1...

Let p(t) = 0.0375t 2 +0.225t be the density function for the shelf life of a brand of banana which lasts up to 4 weeks. Time, t, is measured in weeks and 0 t 4. Find the mean shelf life of a banana...

Let p(t) = 0.0375t 2 +0.225t be the density function for the shelf life of a brand of banana which lasts up to 4 weeks. Time, t, is measured in weeks and 0 t 4. Find the median shelf life of a...

Let p (t) = figure below. fraction of bananas per week of age 0.4 0.3 0.2 0.03751 +0.225t be the density function for the shelf life of a brand of banana, with t in weeks and 0 4. See the 0.1 1 p(t)...

Homework 17. Entire questions are provided. Chapter 7, Section 7.3, Question 001 Suppose you want to analyze the fishing industry in a town. Each day, the boats bring back at least 2 tons of fish,...

Let $p(t)=-0.0390 t^{2}+0.229 t$ be the density function for the shelf life of a brand of banana which lasts up to 4 weeks. Time, $t$, is measured in weeks and $0 \leq t \leq 4$. * Your answer is...

Find attached Ingredients: Water, MCC, Salt, Nicotine, pH regulator, sweeteners and flavours I am wondering why the decision to go with LYFT. I understand migrating to LYFT would be easier from sells...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

contributed articles DOI:10.1145/ 2602574 How to use, and influence, consumer social communications to improve business performance, reputation, and profit. BY WEIGUO FAN AND MICHAEL D. GORDON The...

Using this year-by-year historical data, calculate 3, 5, and 10-year forecasts for each of the rows (i.e. Net Sales, etc., down to Total Shareholders Equity). Please use Spreadsheet. Apple Inc....

There are many vertical market industries with special accounting information needs apart from the industries discussed in this chapter. Identify three additional vertical market industries. What are...

Question 1 0 ( 2 points ) For the Musk project, what is the initial investment in new property, plant and equipment? $ 6 8 0 m m $ 6 6 0 m m $ 3 0 0 m m $ 6 0 0 m m $ 5 9 5 m m

What amount of income tax is withheld from the salary of an employee who is single with three withholding allowances and earnings of $$645$ in a week? (Use the wage bracket withholding table from...

In Exercises, suppose that x and y are related by the given equation and use implicit differentiation to determine dy/dx. x(y + 2) 5 = 8

Differentiate the functions in Exercises using one or more of the differentiation rules discussed thus far. y = (x 2 + 5) 15

Differentiate the functions in Exercises. y 1 x + x + 7 2

Case Study 2 of 3: SQL with Pine Valley Furniture Company Database Business Intelligence and Analytics Your assignment is to write and execute the SQL queries that will produce the data (record sets)...

Your company is undertaking a new project. A building was purchased 5 years ago for $1,200,000 depreciated straight line to $300,000 (the land value) over 30 years. It is now worth $1,600,000...

Table 3-1 Jones Company Financial Information December 2009 December 2010 Net Income $2,000 $4,000 Accounts receivable 750 950 Accumulated depreciation 1,000 1,500 Common stock 4,500 5000 Paid-in...