Suppose that the population density function for a city is 40e^-0.5t thousand people per square mile. Let P(t) be the total population that lives within t miles of the city center, and let Δt be a small positive number.

(a) Consider the ring about the city whose inner circle is at t miles and outer circle is at t + Δt miles. The text shows that the area of this ring is approximately 2πt Δt square miles. Approximately how many people live within this ring? (Your answer will involve t and Δt.)

(b) What does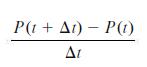

approach as Δt tends to zero?

(c) What does the quantity P(5 + t) - P(5) represent?

(d) Use parts (a) and (c) to find a formula for

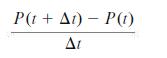
and from that obtain an approximate formula for the derivative P′(t). This formula gives the rate of change of total population with respect to the distance t from the
city center.

(e) Given two positive numbers a and b, find a formula involving a definite integral, for the number of people who live in the city between a miles and b miles of the city center.

P(t + ) - P(t)