Question: The following system of differential equations represents the interaction between two populations, x and y. (a) Describe how the species interact. How would each species

The following system of differential equations represents the interaction between two populations, x and y.

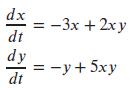
dx dt dy dt = 3x+2xy =-y+5xy

(a) Describe how the species interact. How would each species do in the absence of the other? Are they helpful or harmful to each other?
(b) If x = 2 and y = 1, does x increase or decrease? Does y increase or decrease? Justify your answers.
(c) Write a differential equation involving dy∕dx.
(d) Use a computer or calculator to draw the slope field for the differential equation in part (c).
(e) Draw the trajectory starting at point x = 2, y = 1 on your slope field, and describe how the populations change as time increases.

dx dt dy dt = 3x+2xy =-y+5xy

Step by Step Solution

★★★★★

3.41 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The species need each other to survive Both would die out ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Applied Calculus Questions!

Each system of differential equations is a model for two species that either compete for the same resources or cooperate for mutual benefit (flowering plants and insect pollinators, for instance)....

A disease with classes S, I and Ris represented by the following system of differential equations ds = -BSI + yR, dt dI = BS I - ul, dt (4) %3D dR = ul - yR, dt where B, y and are positive parameters.

please help. not sure how to approach this at all. The following system of differential equations d F: = 0.15;. 0.000232 0.000633; s I? = 0,02,, 0.000083;2 0.000233; where 1: 2 0 and y 2 0, is a...

Consider the following system of differential equations for two species x and y: dx/dt = 0.5 x - 0.001 xy , dy/dt = -0.3y + 0.0001 xy (a) What type of interaction is this ? And why ? (b) What are any...

Recall the Lotka volterra model of predator-prey interactions from the lectures: ()()=()()()=()()() where () is the number of prey, () is the number of predators, and are the birth and death rates of...

1. Campus police are investigating a hit-and-run accident in which the driver of a late- model sports car has run down the statue of a popular mathematics professor. The accident took place at 8:00...

Give the rates of growth of two populations, x and y, measured in thousands. (a) Describe in words what happens to the population of each species in the absence of the other. (b) Describe in words...

Explain the meaning of the following terms in federal accounting: a. Apportionment b. Allotment c. Obligation d. Commitment e. Expended Appropriations

11.40. (t) = -6e

Jennifer owns a 1 0 - year bond with a 5 % coupon. The bond is currently priced at 1 0 1 . What does this indicate about current interest rates? The bond is trading at a premium because current...

=+57. Coffee and doughnuts. At a certain coffee shop, all the customers buy a cup of coffee; some also buy a doughnut. The shop owner believes that the number of cups he sells each day is normally...

Differentiate (with respect to t or x): y = sin(ln t)

Find t such that -/2 t /2 and t satisfies the stated condition. sin t = sin(-4/3)

Differentiate (with respect to t or x): y = (1 + tan 2t) 3

You are trying to decide how much to save for retirement. Assume you plan to save $8,000 per year with the first investment made one year from now. You think you can earn 10.0% per year on your...

Old MathJax webview an example of a permanent account is:

On June 1, 2013 Oakcrest Company signed a three year $110, note payable with 9% interest. Interest is due on June 1 of each year beginning in 2014. What amount of interest expense should be reported...