(a) Explain why the wavelet expansion (9.136) defines a linear transformation on Rn that takes a wavelet coefficient vector c = (c₀, c₁, . . . , c_n−1)^T to the corresponding sample vector f = (f₀, f₁, . . . , f_n−1)^T. 

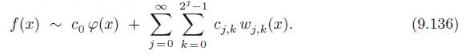
(b) According to Theorem 7.5, the wavelet map must be given by matrix multiplication f = W_n c by a 2 × 2ⁿ matrix W = Wⁿ. Construct W₂, W₃ and W₄. 

(c) Prove that the columns of W_n are obtained as the values of the wavelet basis functions on the 2ⁿ sample intervals. 

(d) Prove that the columns of W_n are orthogonal.

(e) Is W_n an orthogonal matrix? Find a formula for W_n⁻¹.

(f) Explain why the wavelet transform is given by the linear map, c = W_n⁻¹ f.

Theorem 7.5.

Every linear function L:Rⁿ → R^m is given by matrix multiplication, L[v] = Av, where A is an m × n matrix.

2-1 f(x) Cop(a) + AW; (2). j=0 k=0 (9.136)