(a) Under the assumption that u 1 , , u k form a Jordan chain for the coefficient matrix A, prove that the functions (10 17) are solutions to the system u Au (b) Prove that they are linearly independent u1(t) e w1, u (t) e(t w W), u (t) ext and, in general, u(t) e(tw tW2 W3), ti i 1jk (j i) W 23 (10 17)

Question: (a) Under the assumption that u 1 , . . . , u k form a Jordan chain for the coefficient matrix A, prove that

(a) Under the assumption that u₁, . . . , u_k form a Jordan chain for the coefficient matrix A, prove that the functions (10.17) are solutions to the system u̇ = Au.

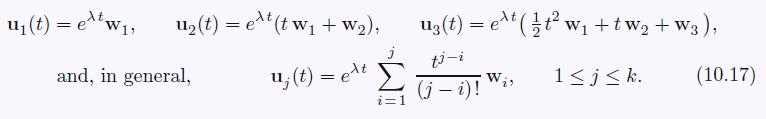
u1(t)=e^w1, u (t) = e(t w + W), u; (t) = ext

(b) Prove that they are linearly independent.

u1(t)=e^w1, u (t) = e(t w + W), u; (t) = ext and, in general, u(t) = e(tw +tW2 + W3), ti-i 1jk. (j-i)! W 23 (10.17)

Step by Step Solution

★★★★★

3.49 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To show that the functions 1017 are solutions to the system u Au we need to verify that they satis... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Applied Linear Algebra Questions!

List three specific parts of the Case Guide, Objectives and Strategy Section (See below) that you had the most difficulty understanding. Describe your current understanding of these parts. Provide...

Consider a 2-person/2-good exchange economy in which person 1 is endowed with (e11, e12) and person 2 is endowed with (e21, e22) of the goods x1 and x2. A: Suppose that tastes are homothetic for both...

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

Can you please help me with number 31. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials and Linear...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Can you please help me with number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Linear Systems quations 406 The...

Can you please help me with number 21. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Open with Chapter 5 Linear Systems...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.6 Problems Find...

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

(iii) Now express your decision rule instead using only the quantities p(Ck), p(Cj ), p(x|Ck), p(x|Cj ), and relate it to the diagram above. [2 marks] (iv) If the classifier decision rule assigns...

1- Triacylglycerides from the diet are converted in the intestinal mucosa into: a) Lipoproteins b) Chylomicrons c) Unsaturated fatty acids d) Ketone bodies e) Saturated fatty acids

? ? Answer each question using the time value of money table. (Show me the steps of solving, writing the answers only are not acceptable). 1. If you deposit money today into an account that pays 6...

More people throughout the world visit the cinema. What impact is this likely to have on the demand for actors and their wages? Demand for actors Wages of actors A decreases decrease B decreases...

Which entity will meet the following requirements? 1.. Availability of preferred returns for certain investors. 2.. Considers loans from third parties in basis of owners. 3.. Limited liability. a....

Use orthogonality to write the polynomials 1, x and x2 as linear combinations of the orthogonal basis (5.1).

(a) Prove that the polynomials form an orthogonal basis for the vector space P3 of cubic polynomials for the L2 inner product (b) Find an orthonormal basis of V3. (c) Write t3 as a linear combination...

(a) Prove that the polynomials form an orthogonal basis for P2 with respect to the weighted inner product (b) Find the corresponding orthonormal basis. (c) Write t2 as a linear combination of P0, P1,...

VANISHING GAMES CORPORATION Trial Balance January 31, 2021 Account Title Debit Credit Cash 1,431,500 Accounts Receivable 212,500 Supplies 17,700 Land 1,200,000 Buildings 422,000 Equipment 908,000...

Explain the common forms of business ownership sole proprietorship, partnership, and corporation and demonstrate how they differ in terms of owners' equity presentation.

Journal Entries for : 1. record issuance of raw materials. 2 direct labor incurred . 3. Apply manufacturing overhead . 4.work completed in Cooking department . 5 work completed in Molding department...