Let H_n = Q_nR_n be the QR factorization of the n × n Hilbert matrix (1.72). 

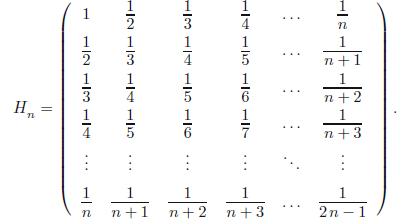
(a) Find Q_n and R_n for n = 2, 3, 4.

(b) Use a computer to find Q_n and Rn for n = 10 and 20.(c) Let x^⋆ ∈ Rⁿ denote the vector whose i^th entry is x^⋆_i = (−1)ⁱ i/(i + 1). For the values of n in parts (a) and (b), compute y^⋆ = H_nx^⋆. Then solve the system H_nx = y^⋆ 

(i) Directly using Gaussian Elimination;

(ii) Using the QR factorization based on(4.34);

(iii) Using Householder’s Method. Compare the results to the correct solution x^⋆ and discuss the pros and cons of each method.