Question: Let u 1 , . . . , u n and u 1 , . . . , u n be orthonormal bases of an

Let u1, . . . , un and û1, . . . , ûn be orthonormal bases of an inner product space V.


Prove that 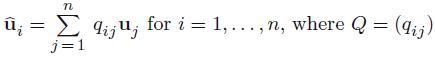= n qijj j=1 qiju, for i = 1,..., n, where Qis an orthogonal matrix.

= n qijj j=1 qiju, for i = 1,..., n, where Q = (ij)

Step by Step Solution

★★★★★

3.34 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

ANSWER To prove that the matrix Q qij is an orthogonal matrix we need to show that QQT I where I is ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Applied Linear Algebra Questions!

Q:

Let W be a subspace of an inner product space V and let {w1, w2, ... wm} be an orthogonal basis for W. Show that if v is any vector in V, then (v, wi) (v, w2) (V, W res

Q:

Let V be an inner product space and u a fixed vector in V. Prove that the set of all vectors in V that are orthogonal to u is a subspace of V.

Q:

Let v be a vector in an inner product space V. (a) Show that ||v|| > ||projU(v)|| holds for all finite dimensional subspaces U. [Hint: Pythagoras' theorem.] If {e1,e2,..., ew} is any orthogonal set...

Q:

1. (5 pts) Let u=(U1, Uz) and V=(V1, V2) be vectors in R? under traditional vector addition and scalar multiplication. Is the following operation an inner-product? March through the 4 axioms listed...

Q:

2. [25pts] (a) [9 pts) Show that the dual space (Co)' is isometrically isomorphic to l' (here co is a subspace of 1 consisting of sequences of scalars converging to zero). P.T.O 2 ZEZ (b) [8 pts)...

Q:

Let V be an inner product space. Prove that if u and v are any vectors in V, then ||u + v||2 = ||u||2 + ||v||2 if and only if (u, v) = 0, that is, if and only if u and v are orthogonal. This result...

Q:

1. Let B = (v1, .... Un), C= {ul,....un}, and D = (w1,..., Win} be three bases for R". (a) Prove the following identity regarding the change of basis matrices: Pc +DPBAC = l'B +D. (b) Consider the...

Q:

Theorem 6.14 (Schur). Let T be a linear operator on a nite- dimensional inner product space V. Suppose that the characteristic poly- nomial of T splits. Then there exists an orthonormal basis 7 for V...

Q:

3. Prove or disprove the following statements. (a) If v1, . . ., Un are orthonormal in an inner product space V, then II Et-, vill = vn. (b) Let P be an n x n matrix. If {v1, ..., Un} and {PU1, ...,...

Q:

9. Let T be a linear operator on a nite-dimensional vector space V, and suppose there exists an ordered basis if for V such that [T] 5 is an upper triangular matrix. (a) Prove that the characteristic...

Q:

Consider one year as one period. Assume that the 1-year and 2-year spot rates are 2% and 2.2%, respectively. Assume that one year from now, the 1-year spot rate will be either 1.8% or 2.5% with equal...

Q:

Harrington Corporation needs to set a target price for its newly designed product R2D2. The following data relate to this new product. These costs are based on a budgeted volume of 100,000 units...

Q:

Nature Gnome Company Balance Sheet 3 1 - Dec - 2 4

Q:

The federal funds rate is the interest rate charged by banks when banks borrow overnight from each other. The file titled The Fed contains the federal funds rates for the period 19552015 (source:...

Q:

Suppose A is a nonsingular n x n matrix. (a) Prove that any n x (n + k) matrix of the form (A B), where B has size n à k. has rank n. (b) Prove that any (n + k) à n matrix of the form...

Q:

Let A be an m x n matrix of rank r. Suppose v1,. . . vn are a basis for Rn such that vr+1.......vn form a basis for ker A. Prove that w1 = Av1.... . wr = Avr, form a basis for mg A.

Q:

(a) Suppose A.B are m x n matrices such that ker A = ker B. Prove that there is a nonsingular m m matrix M such that MA = B. (b) Use this to conclude that if Ax = b and Bx = c have the same...

Q:

To obtain an approximate estimate of the NOMINAL interest rate, one must _________ the __________ the real risk-free rate. Group of answer choices A. add; default premium to B. subtract; default...

Q:

Selected current year-end financial statements of Cabot Corporation follow. (All sales were on credit; selected balance sheet amounts at December 31 of the prior year were inventory, $51,900; total...

Q:

A firm just paid a $2.55 per share dividend. If dividends will increase 4% annually, forever, and investors require a 14.75% rate of return, then what is the price of the stock in 4 years? Round to...