State and prove a counterpart to Definition 10.32 and Theorem 10.33 for a homogeneous linear iterative system.

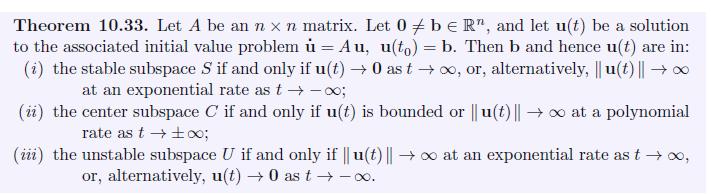
Definition 10.32. Let A be a real n x n matrix. We define the following invariant sub- spaces spanned by the real and imaginary parts of the eigenvectors and Jordan chains corresponding to the eigenvalues with the following properties: (i) negative real part: the stable subspace SCR"; (ii) zero real part: the center subspace CCR"; (iii) positive real part: the unstable subspace U CR".