As displayed in Fig. P13.6, an LC circuit can be modeled by the following system of differential equations:

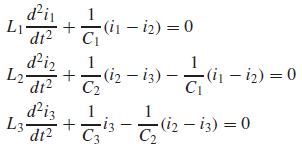
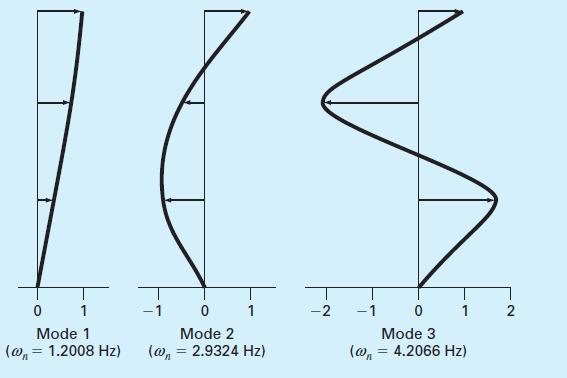
where L = inductance (H), t = time (s), i = current (A), and C = capacitance (F). Assuming that a solution is of the form i_j = I_j sin (ωt), determine the eigenvalues and eigenvectors for this system with L = 1 H and C = 0.25C. Draw the network, illustrating how the currents oscillate in their primary modes.

LI z+P + (1-12) = 0 dfiz d12 di3 L3 + d12 L2- + (12-13) - (11-12) = 0 - 2(2-13) = 0