Develop an M-file function to determine the largest eigenvalue and its associated eigenvector with the power method. Test the program by duplicating Example 13.3 and then use it to solve Prob. 13.2.

Example 13.3

Data From Problem 13.2

Use the power method to determine the highest eigenvalue and corresponding eigenvector for

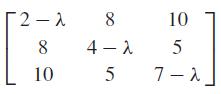
Power Method for Highest Eigenvalue Problem Statement. Using the same approach as in Section 13.2, we can derive the fol- lowing homogeneous set of equations for a three mass-four spring system between two fixed walls: 2k (2h - 60) X -X m1 2k - X + (1 - 0) X m2 m2 -X + m3 - 40 -20 0 -20 40 -20 - [1] = 0 0 -20 40 m2 - (12/12 - 0) X M3 = 0 -X3=0 X3 = 0 If all the masses m = 1 kg and all the spring constants k = 20 N/m, the system can be expressed in the matrix format of Eq. (13.4) as where the eigenvalue is the square of the angular frequency . Employ the power method to determine the highest eigenvalue and its associated eigenvector.