Develop an M-file to solve a single ODE with Heun’s method with iteration. Design the M-file so that it creates a plot of the results. Test your program by using it to solve for population as described in Prob. 22.5. Employ a step size of 5 years and iterate the corrector until ε_s 

Data From Problem  22.5

 In such cases, the growth rate is not a constant,  but can be formulated as

k_g = k_gm(1 − p/pmax)

where k_gm = the maximum growth rate under unlimited conditions, p = population, and p_max = the maximum population. Note that pmax is sometimes called the carrying capacity. Thus, at low population density p ≪ pmax, k_g → k_gm. As p approaches p_max, the growth rate approaches zero. Using this growth rate formulation, the rate of change of population can be modeled as

This is referred to as the logistic model. The analytical solution to this model is

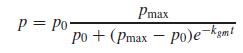
dp dt = kgm (1-P/Pmax) P