The following infinite series can be used to approximate e x : (a) Prove that this Maclaurin
Question:
The following infinite series can be used to approximate ex:
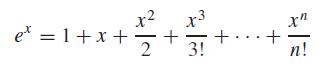
(a) Prove that this Maclaurin series expansion is a special case of the Taylor series expansion (Eq. 4.13) with xi = 0 and h = x.
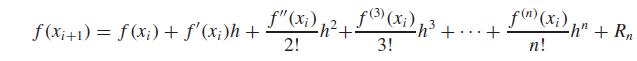(b) Use the Taylor series to estimate f (x) = e−x at xi + 1 = 1 for xi = 0.25. Employ the zero-, first-, second-, and third-order versions and compute the |εt| for each case.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
ANSWER a To show that the given Maclaurin series expansion is a special case of the Taylor series ex...View the full answer
Answered By
User l_917591
As a Business Management graduate from Moi University, I had the opportunity to work as a tutor for undergraduate students in the same field. This experience allowed me to apply the theoretical knowledge I had gained in a practical setting, while also honing my teaching and communication skills.
As a tutor, I was responsible for conducting tutorial sessions, grading assignments and exams, and providing feedback and support to my students. I also assisted with the preparation of course materials and collaborated with other tutors and professors to ensure consistency in teaching and assessment.
0 Reviews
10+ Question Solved
Related Book For 
Applied Numerical Methods With MATLAB For Engineers And Scientists
ISBN: 9781259027437
3rd Edition
Authors: Steven C. Chapra
Question Posted:
