Consider the inspection described in Example 2.11. From a bin of 50 parts, 6 parts are selected randomly without replacement. The bin contains 3 defective parts and 47 nondefective parts. What is the probability that exactly 2 defective parts are selected in the sample?

Example 2.11

A bin of 50 manufactured parts contains 3 defective parts and 47 nondefective parts. A sample of 6 parts is selected without replacement. That is, each part can be selected only once, and the sample is a subset of the 50 parts. How many different samples are there of size 6 that contain exactly 2 defective parts?

A subset containing exactly 2 defective parts can be formed by first choosing the 2 defective parts from the 3 defective parts. Using Equation 2.4, the number of different ways this step can be completed is

\[ \left(\begin{array}{l} 3 \\ 2 \end{array}\right)=\frac{3 !}{2 ! 1 !}=3 \]

Equation 2.4

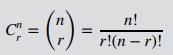
C (c) n! r!(n-r)!