Let 1 n 1 n be the vector in R n R n whose components are all one. Show that J n = J n

Let $1_n$ be the vector in $R^n$ whose components are all one. Show that $J_n=$ $1_n{1}_n^{\prime }/n$ is a projection matrix, i.e., that $J_n^2=J_n$, and that it has rank one: tr(J_n) = 1$\text{Extra left or missing right}$. Show also that $I_n-J_n$ is the complementary projection of rank $n-1$.

Each of the quadratic forms in Exercise 1.15 can be expressed in the form $Y^{\prime }{M}_{r}Y$, where each $M_r$ is a projection matrix of order $mn\times mn$. Show that each matrix is a Kronecker product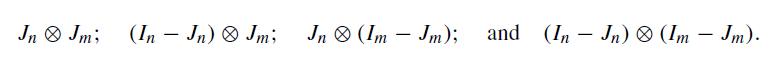

Find the rank of each matrix.

Exercise 1.15

- Jn Jm; (InJn) Jm; Jn (Im Jm); (I) and (In Jn) (Im - Jm).