Let X₁, X₂, €¦ , X_nbe uniformly distributed on the interval 0 to a. Recall that the maximum likelihood estimator of a is aÌ‚ = max(X_i).

(a) Argue intuitively why ˆa cannot be an unbiased estimator for a.

(b) Suppose that E(â) = na / (n +1). Is it reasonable that â consistently underestimates a? Show that the bias in the estimator approaches zero as n gets large.

(c) Propose an unbiased estimator for a.

(d) Let Y = max(Xi ). Use the fact that Y ‰¤ y if and only if each Xi ‰¤ y to derive the cumulative distribution function of Y . Then show that the probability density function of Y is

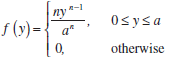
Use this result to show that the maximum likelihood estimator for a is biased.

(e) We have two unbiased estimators for a: the moment estimator aÌ‚ = 2XÌ… and aÌ‚ = [(n + 1)] /n max(X_i), where max(X_i ) is the largest observation in a random sample of size n. It can be shown that V(aÌ‚ ) = a² / (3n) and that V (aÌ‚ ) = a² / [n(n + 2)]. Show that if n > 1, aÌ‚₂ is a better estimator than aÌ‚. In what sense is it a better estimator of a?

f (y)= - 0, Osysa a" otherwise