Question: This exercise extends the hypergeometric distribution to multiple variables. Consider a population with N items of k different types. Assume that there are N 1
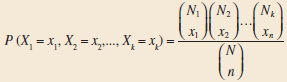
NE X1 P (X, = x,, X, = x,.., X, = x,) = C) X2 ,
Step by Step Solution
3.48 Rating (184 Votes )
There are 3 Steps involved in it
The probability function for X is The number of ways to ... View full answer

Get step-by-step solutions from verified subject matter experts


