Equation (14.1) on page 513 defines the joint distribution represented by a Bayesian network in terms of the parameters θ(X_i|Parents(X_i)). This exercise asks you to derive the equivalence between the parameters and the conditional probabilities P(X_i|Parents(X_i)) from this definition.

a. Consider a simple network X †’ Y †’ Z with three Boolean variables. Use Equations (13.3) and (13.6) (pages 485 and 492) to express the conditional probability P(z | y) as the ratio of two sums, each over entries in the joint distribution P(X, Y, Z). 

b. Now use Equation (14.1) to write this expression in terms of the network parameters θ(X), θ(Y |X), and θ(Z | Y ).

c. Next, expand out the summations in your expression from part (b), writing out explicitly the terms for the true and false values of each summed variable. Assuming that all network parameters satisfy the constraint ˆ‘_xi θ(xi | parents(X_i)) = 1, show that the resulting expression reduces to θ(x | y).

d. Generalize this derivation to show that θ(X_i |Parents(X_i)) = P(X_i |Parents(X_i)) for any Bayesian network.

Equation (14.1)

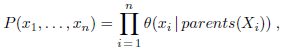
Equations (13.3)

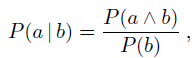
Equations (13.6)

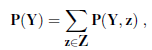
P(r1,..., In) = | 9(x;|parents(X;)), i=1 () P(a|b) P(b)