Prove that more informed heuristics develop the same or less of the search space. formalize the argument presented in Section 4.3.3.

Data from section 4.3.3

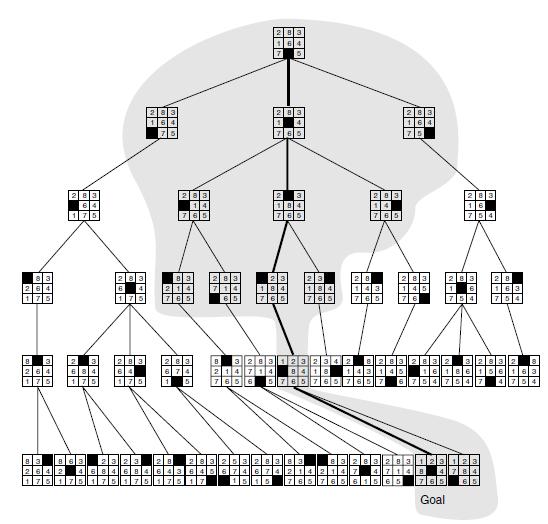
The final issue of this subsection compares two heuristics' ability to find the minimal path. An interesting case occurs when the heuristics are A*. DEFINITION INFORMEDNESS For two A* heuristics h, and h, if h,(n) h(n), for all states n in the search space, heuristic h is said to be more informed than h. We can use this definition to compare the heuristics proposed for solving the 8-puzzle. As pointed out previously, breadth-first search is equivalent to the A* algorithm with heuristic h, such that h(x) = 0 for all states x. This is, trivially, less than h*. We have also shown that h, the number of tiles out of place with respect to the goal state, is a lower bound for h*. In this case h, h h*. It follows that the "number of tiles out of place" heuristic is more informed than breadth-first search. Figure 4.18 compares the spaces searched by these two heuristics. Both h, and h find the optimal path, but h evaluates many fewer states in the process. Similarly, we can argue that the heuristic that calculates the sum of the direct distances by which all the tiles are out of place is again more informed than the calculation