Elliptic curve cryptography uses equations of the form y² = x³ + ax + b and a type of point addition where the “sum” R of points P and Q is found by extending a line through P and Q, determining the third point where the line intersects the curve, and then reflecting that point across the x-axis. For the curve y² = x³ − 6x + 9, find the coordinates of point R for P(−3, 0) and Q(0, 3). See Fig. 15.12.

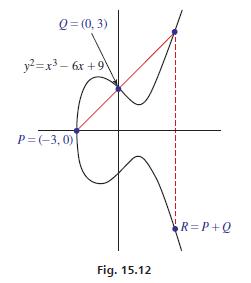
Q = (0, 3) y=x-6x +9\ P=(-3,0) Fig. 15.12 R=P+Q