In Example 1, change the 9 to 36; find the vertices, ends of the minor axis, and foci; and sketch the ellipse.

Data from Example 1

The ellipse

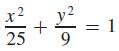
seems to fit the form of either Eq. (21.17) or Eq. (21.19).

Because a² = b² + c², we know that a is always larger than b.
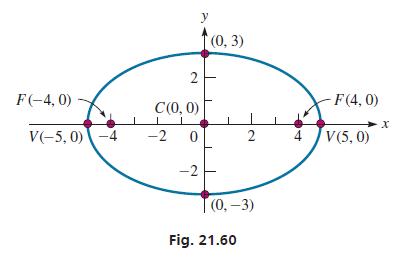
Because the square of the larger number appears under x 2, we know the equation is in the form of Eq. (21.17). Therefore, a² = 25 and b² = 9, or a = 5 and b = 3. This means that the vertices are (5, 0) and (−5, 0), and the minor axis extends from (0,−3) to (0, 3). See Fig. 21.60. 

We find c from the relation c² = a² − b². This means that c² = 16 and the foci are (4, 0) and (−4, 0).

2 X 25 9 1