In Example 2, change 5/13 to 12/13 and then find the value of cos( + ). Data from Example 2 Given that sin = 5/13

In Example 2, change 5/13 to 12/13 and then find the value of cos(α + β).

Data from Example 2

Given that sinα = 5/13 (α in the first quadrant) and sin β = − 3/5 (for β in the third quadrant), find cos(α + β).
Because sin α = 5/13 for α in the first quadrant, from Fig. 20.7, we have cos α = 12/3 Also, because sin β = − 3/5 for β in the third quadrant, from Fig. 20.7, we also have cos β = −4/5

Then, by using Eq. (20.10), we have

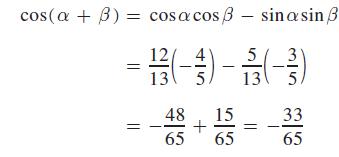
cos(a + 3) = cosacos B - sinasin 3 4 5 3 = (-1) - (-) 12 13 5 13 || 48+15=-33 65 65 65