In Example 3, change the fourth and fifth terms from −4y − 4 to +6y − 9 and then find the center.

Data from Example 3

Find the center of the hyperbola 2x² − y² − 4x − 4y − 4 = 0. To analyze this curve, we first complete the square in the x-terms and in the y-terms. This will allow us to recognize the values of h and k.

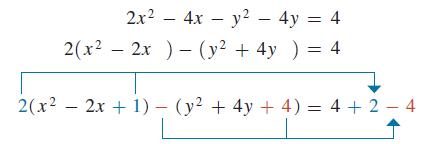
[We note here that when we added 1 to complete the square of the x-terms within the parentheses, we were actually adding 2 to the left side. Thus, we added 2 to the right side. Similarly, when we added 4 to the y-terms within the parentheses, we were actually subtracting 4 from the left side. Thus, we subtract 4 from the right side.] Continuing, we have

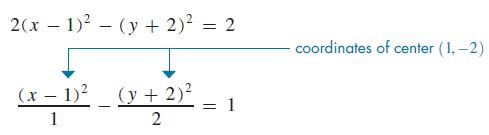
Therefore, the center of the hyperbola is (1,−2). See Fig. 21.86.

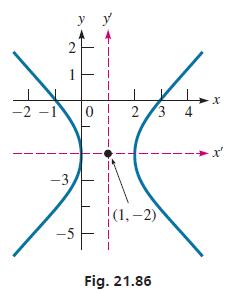
2x - 4x - y - 4y = 4 - (y + 4y) = 4 2(x2x) 2(x- 2x + 1) (y + 4y + 4) = 4+2 - 4