In Example 3(a), change 4y to −6y.

Data from Example 3(a)

The parabola x² = 4y fits the form of Eq. (21.16). Therefore, its axis is along the y-axis and its vertex is at the origin. From the equation, we find the value of p, which in turn tells us the location of the vertex and the directrix.

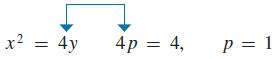
Focus (0, p) is (0, 1); directrix y = −p is y = −1. The parabola is shown in Fig. 21.47, and we see in this case that it opens upward.

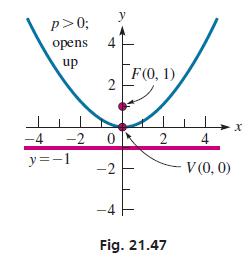
x = 4y 4p = 4, P = 1