In Example 5, change 3 to −3 and −5 to 5.

Data from Example 5

Using Eq. (21.42), we can transform the rectangular coordinates (3,−5) into polar coordinates, as follows.

We know that θ is a fourth-quadrant angle because x is positive and y is negative. Therefore, the point (3,−5) in rectangular coordinates can be expressed as the point (5.83, 5.25) in polar coordinates (see Fig. 21.108). Other polar coordinates for the point are also possible.

Calculators are programmed to make conversions between rectangular and polar coordinates. The display for the conversions of Examples 4 and 5 are shown in Fig. 21.109.

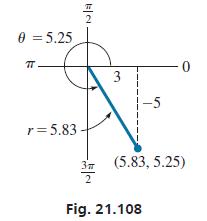
tan = ] = 5 3 9 = 5.25 (or 1.03) 32+(-5)2 = 5.83