In Example 5, change the + sign before the 5x to −.

Data from Example 5

Find the roots of the equation 2x³ + x² + 5x − 3 = 0. Because n = 3, there are three roots. If we can find one of these roots, we can use the quadratic formula to find the other two. We have

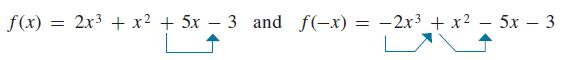
which shows there is one positive root and no more than two negative roots, which may or may not be rational. The possible rational roots are ±1, ±1/2, ±3/2, ±3. First, trying the root 1 (always a possibility if there are positive roots), we have the synthetic division shown at the left. The remainder of 5 tells us that 1 is not a root, but we have gained some additional information, if we observe closely. If we try any positive number larger than 1, the results in the last row will be larger positive numbers than we now have. The products will be larger, and therefore the sums will also be larger. Thus, there is no positive root larger than 1. This leads to the following rule: [When we are trying a positive root, if the bottom row contains all positive numbers, then there are no roots larger than the value tried.] This rule tells us that there is no reason to try +3/2 and +3 as roots. (It is also true that when trying a negative root, if the signs alternate in the bottom row, then there are no roots less than the value tried.)

Now let us try + 1/2, as shown at the left. The zero remainder tells us that + 1/2, is a root, and the remaining factor is 2x² + 2x + 6, which itself factors to 2(x² + x + 3). By the quadratic formula, we find the remaining roots by solving the equation x² + x + 3 = 0. This gives us

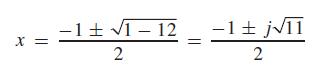
The three roots are

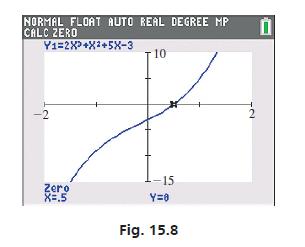
There are no negative roots because the nonpositive roots are complex. Proceeding this way, we did not have to try any negative roots. The calculator display in Fig. 15.8 verifies the one real root at x = 1/2.

Transcribed Image Text:

f(x) = 2x³ + x² + 5x - 3 and f(-x) = -2x³ + x² - 5x - 3 ↑