In Example 7, what changes occur if the 6 in the first equation is changed to a 2?

Data from Example 7

Solve the system of equations

x = 2y + 6

6y = 3x - 6

Writing each of these equations in slope-intercept form, we have for the first equation

For the second equation, we have

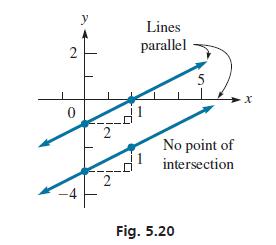
From these, we see that each line has a slope of 1/2 and that the y-intercepts are (0, −3) and (0, −1). Therefore, we know that the y-intercepts are different, but the slopes are the same. Because the slope indicates that each line rises 1/2 unit for y for each unit x increases, the lines are parallel and do not intersect, as shown in Fig. 5.20.

y = x - 3 1