In Exercise 44 of Section 16.2, we saw that the matrix multiplication

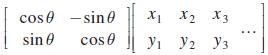
rotates the points in the second matrix counterclockwise about the origin by angle θ. If we replace the first matrix with its inverse, it has the opposite effect of rotating clockwise by angle . The vertices of a triangle in a graphic design program are at (√2, 0), (−√2, 0), and (0,√2). If the triangle is rotated clockwise about the origin by 45°, find the new coordinates of the vertices.

Data from Exercise 44 of Section 16.2.

To rotate a set of points (x₁, y₁), (x₂, y₂), (x₃, y₃), . . . counterclockwise about the origin by angle θ, we multiply 

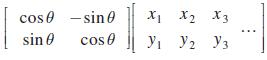
If a photo on a computer screen has corners at (4, 2), (−4, 2), (−4,−2), and (4,−2), find the coordinates of the corners after the photo has been rotated counterclockwise about the origin by 30°.

cos0 -sin sin 0 cos X1 X2 X3 1