Referring to Example 5, show that if the difference in loudness of two sounds is d decibels, the louder sound is 10d /10 more intense than the quieter sound.

Data from Example 5

The human ear responds to sound on a scale that is approximately proportional to the logarithm of the intensity of the sound. Therefore, the loudness of sound (measured in dB) is defined by the equation b = 10 log(I /I₀), where I is the intensity of the sound and I₀ is the minimum intensity detectable.

A busy street has a loudness of 70 dB, and riveting has a loudness of 100 dB. To find how many times greater the intensity I_r of the sound of riveting is than the intensity I_c of the sound of the city street, we substitute in the above equation. This gives

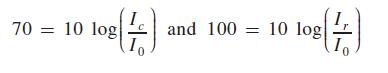
To solve for I_c and I_r we divide each side by 10 and then use exponential form:

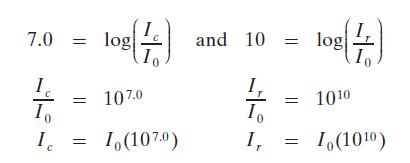
Because we want the number of times I_r is greater than I_c we divide I_r by I_c:

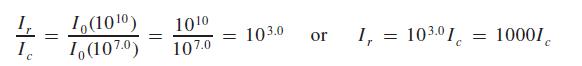
Thus, the sound of riveting is 1000 times as intense as the sound of the city street.

70 10 log 10 log = 0 and 100 = 10 log ( 0