Simplify the given expressions and then check your answers with a calculator as in Example 8.

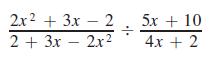
Data from Example 8

To graphically check the result of Example 7, we first let y₁ equal the original expression and y₂ equal the final result. In this case,

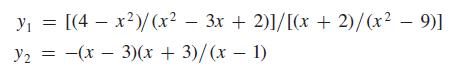
Figure 6.2(a) shows y₂ (in red) being graphed right over y₁ (in blue). Since the graphs are the same, we can consider this as a check (but not as a proof) that the expressions are equivalent.

The table in Fig. 6.2(b) also shows the expressions are equivalent throughout their common domains since the y-values, when they exist, are the same for y₁ and y₂. The x-values that cause division by zero in either function have undefined y-values and are shown as “ERROR” in the table. It is important to note that although the two functions agree with each other, their domains are different.

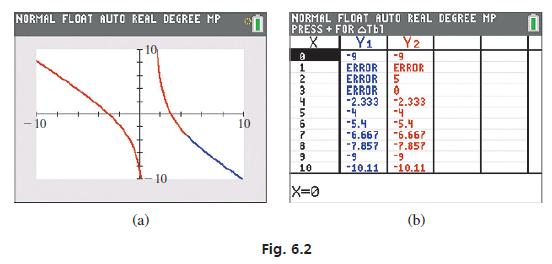
2x + 3x - 2 2 + 3x - 2x 5x +10 4x + 2