Solve the given systems of equations by determinants. All numbers are accurate to at least two significant digits.

The area of a quadrilateral is

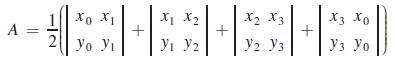
where (x₀, y₀), (x₁ , y₁), (x₂, y₂), and (x₃, y₃) are the rectangular coordinates of the vertices of the quadrilateral, listed counterclockwise. (This surveyor’s formula can be generalized to find the area of any polygon.)

A surveyor records the locations of the vertices of a quadrilateral building lot on a rectangular coordinate system as (12.79, 0.00), (67.21, 12.30), (53.05, 47.12), and (10.09, 53.11), where distances are in meters. Find the area of the lot.

X3 X0 - D A = Xo X1 yo y + X1 X2 1 + X2 X3 +