Solve the given systems of equations by using the inverse of the coefficient matrix. Use a calculator to perform the necessary matrix operations and display the results and the check. See Example 4.

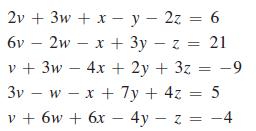
Data from Example 4

Use a calculator to perform the necessary matrix operations in solving the following:

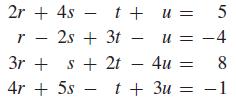
First, we set up matrices A, X, and C:

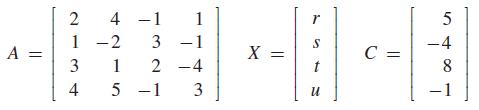
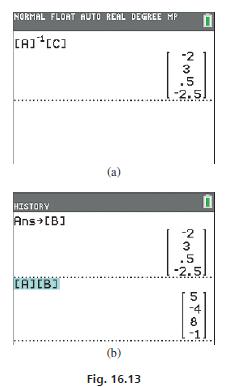
It is now necessary only to enter matrices A and C in the calculator and find the matrix product A⁻¹C, as shown in Fig. 16.13(a). (There is no need to record or display A−1.) This shows that the solution is

This solution can be checked on the calculator by storing the resulting matrix X as matrix B and finding the matrix product AB, which should equal matrix C as shown in Fig. 16.13(b). The product AB is equivalent to substituting each value into the original equations, as shown in Eq. (16.8).

2v + 3w + x - y = 2z = 6 2wx + 3y - z = 21 6v v + 3w - 4x + 2y + 3z = -9 3v w x + 7y + 4z = 5 v + 6w + 6x - 4y - z = -4 -